Evaluating LLM prompts using Adaptive Random Testing
for quickly finding test inputs that reveal "problems" with the prompts
In this post, I will explain one promising technique for evaluating LLM prompts. This technique relies on Adaptive Random Testing (ART), which I have explained separately in this post:
Adaptive Random Testing Introduction
This is a practical explanation of adaptive random testing (ART). We’ll build intuition with tiny, concrete examples. At the end of this post, I will give a brief example using Python.
FYI, the following paper introduces explains this approach too1. However, in this article, I provide a simple, step-by-step guide and code to help you get started integrating this approach into your LLM evaluation workflow.
Why ART for evaluating LLM prompts?
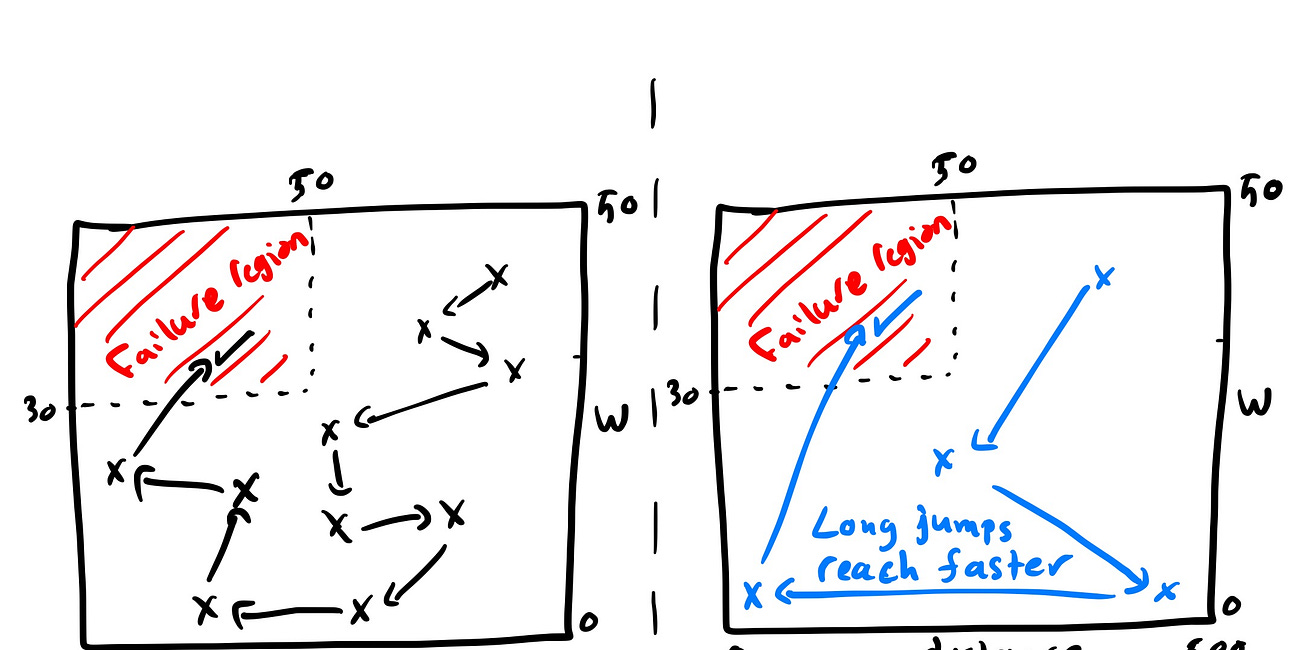
ART attempts to distribute test inputs evenly across the input space, so the evaluation does not cluster around familiar or similar cases.
We can think of prompts as functions, the fixed part is the prompt instructions, and the variable part is the inputs / context.
ART find samples of the input that help us cover far-apart sections of the input space, thus, potentially findings prompt issues faster.
Approach:
Code: https://github.com/khaled-e-a/semantics-systems/blob/main/llm-art-1/llm_art_demo.py
The approach follows the standard structure of Adaptive Random Testing.
We define the space of possible inputs, generate an initial random sample, then iteratively select new inputs that lie far from all previously tested ones.
Each new sample probes a different region of the input space, which increases the chance of revealing prompt failures early.
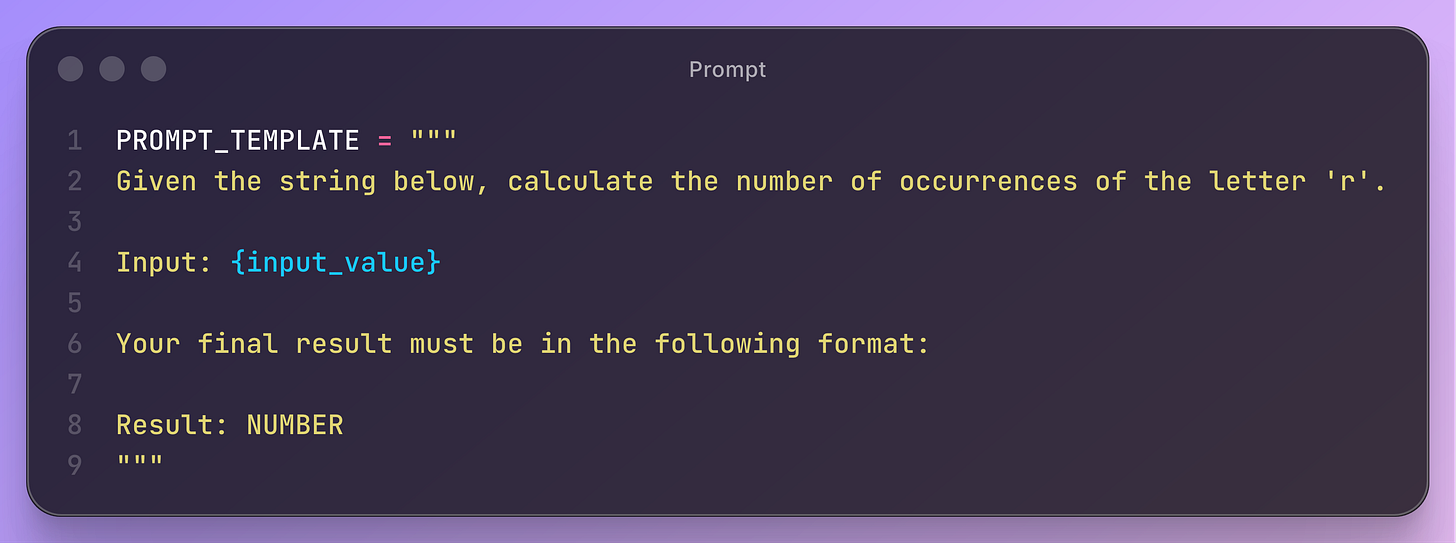
The motivating example uses a simple counting task.
The prompt under test instructs the model to count the number of occurrences of the letter “r” in an input string.
This task is deterministic, easy to check, and sensitive to small variations in the input.
These properties make it suitable for illustrating how ART samples diverse cases and detects errors when the model misinterprets the instruction or miscounts characters.
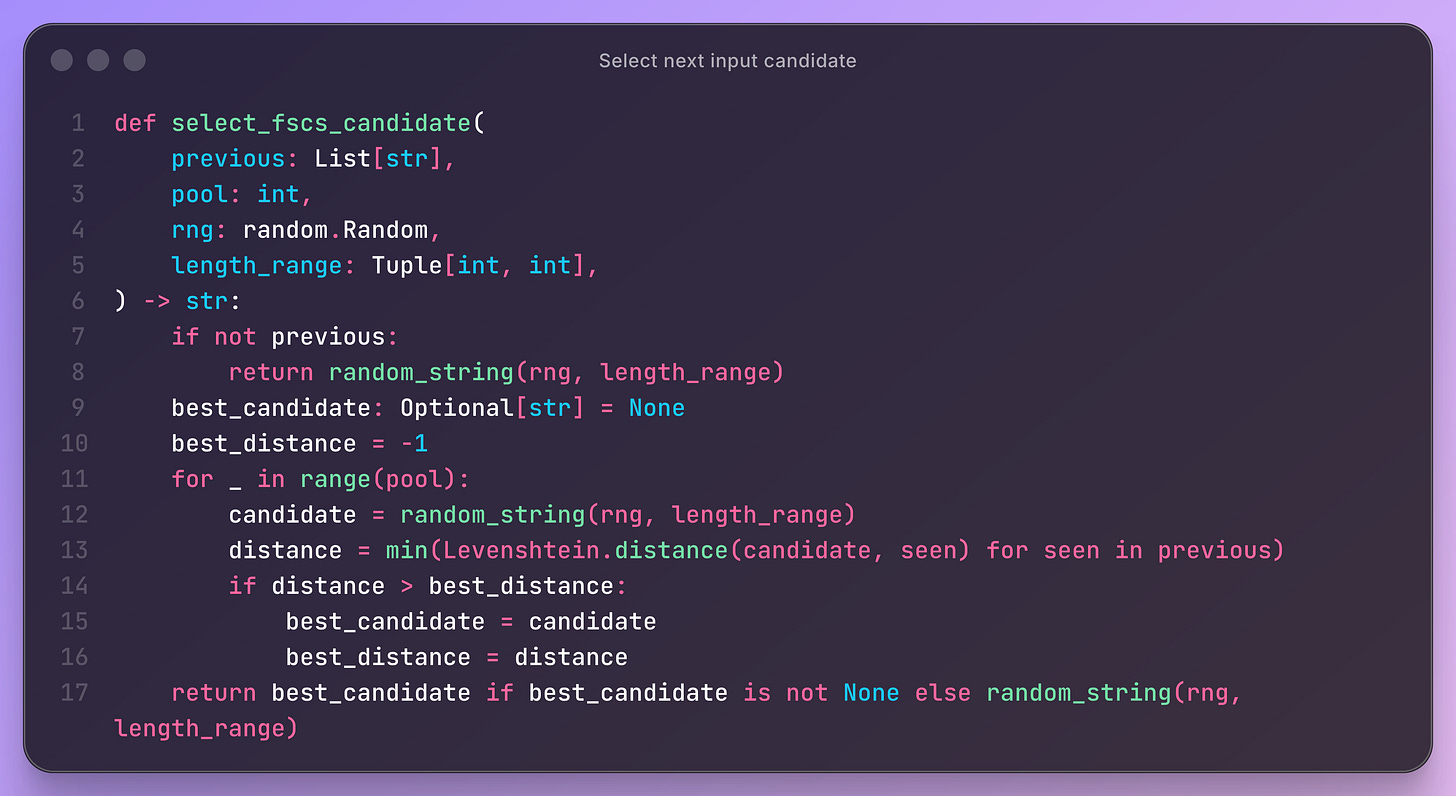
One of the simplest algorithm to select the next prompt input for testing the prompt is the Fixed-Size Candidate Set (FSCS) algorithm.
It implements a single rule: For each new test input, it draws a small pool of random candidates, computes the distance from each candidate to all previously tested inputs, and selects the one whose closest neighbor is as far away as possible.
This distance is computed using the Levenshtein metric, which measures how many edits separate two strings. A candidate with a large minimum distance explores a new region of the input space and improves input diversity.
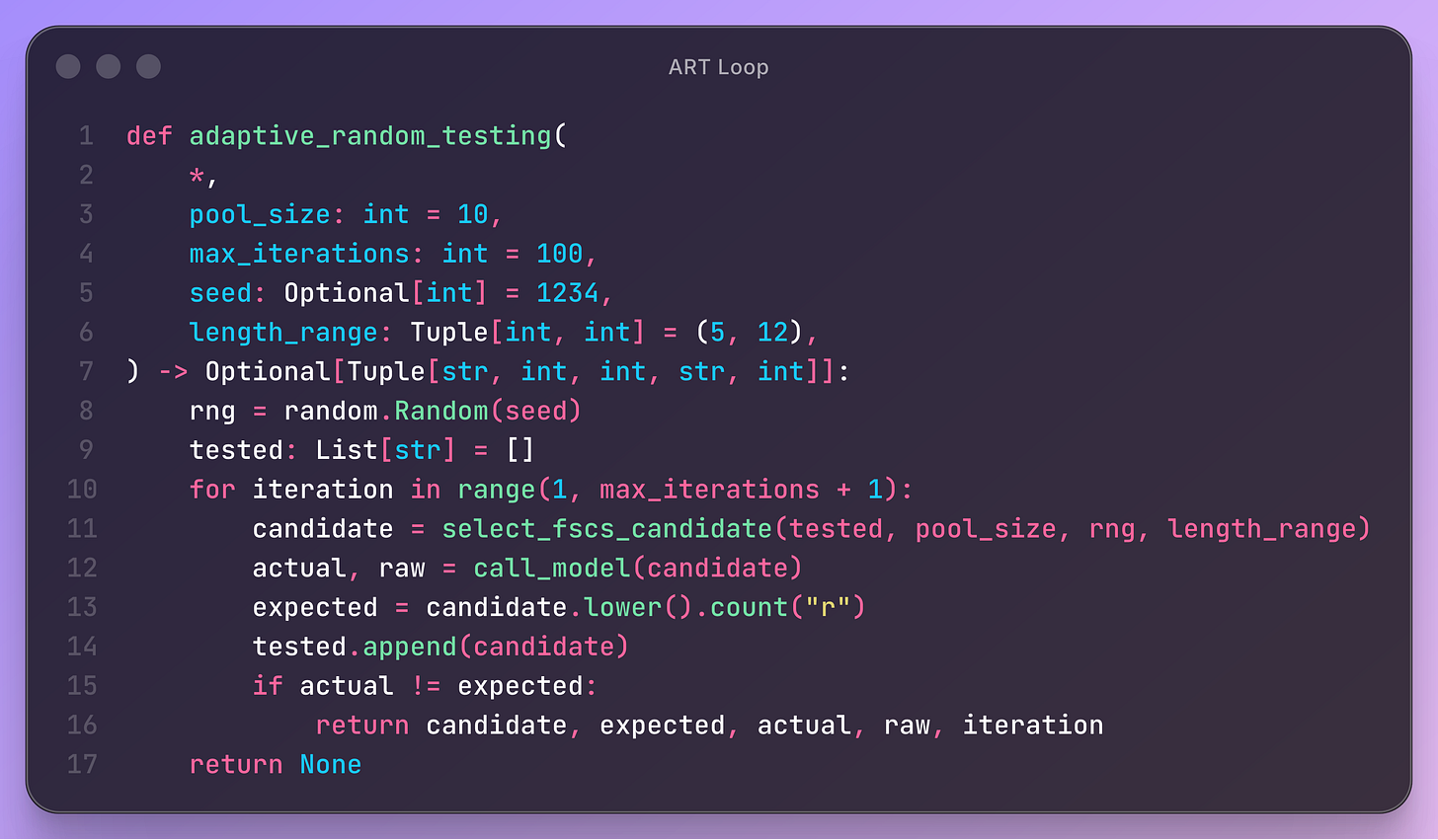
The main ART loop maintains a list of all previously tested inputs.
At each iteration, it uses the FSCS rule to propose a new candidate. It then evaluates the model on that candidate, computes the expected result by directly counting occurrences of “r”, and compares both values.
If a mismatch is found, the loop stops and reports the failure. If no failure is found after the maximum number of iterations, the procedure returns no counterexample.
Each iteration therefore performs one complete cycle: select candidate, evaluate model, check correctness, record test, and continue exploration. This structure mirrors standard test generation workflows, but with a distance-guided selection step that distributes tests more evenly.
Finally, using ART, we are able to identify a failing case:
You can run the code using the command python llm_art_demo.py (after installing all dependencies) .
Conclusions
Adaptive Random Testing offers a structured way to explore prompt behavior.
The FSCS rule ensures that each test probes a new region of the input space, which increases the probability of encountering systematic prompt failures.
Even simple tasks, such as character counting, reveal how distribution-aware sampling can expose subtle defects earlier than uniform random testing.
As LLMs grow in complexity, such systematic evaluation strategies help maintain confidence in prompt reliability and guide prompt refinement in a disciplined way.
Yoon J, Feldt R, Yoo S. Adaptive testing for LLM-based applications: A diversity-based approach. In2025 IEEE International Conference on Software Testing, Verification and Validation Workshops (ICSTW) 2025 Mar 31 (pp. 375-382). IEEE.